Mehr als 40 Jahre sind vergangen, seit Stini und Müller mit großer Eindringlichkeit auf die unbedingte Notwendigkeit von Großversuchen in der Ingenieurgeologie und Felsmechanik hingewiesen haben. Durch sachliche Darlegungen ist das Warum und Wie von Großversuchen, insbesondere solcher zur Feststellung von Festigkeitseigenschaften, erörtert und überzeugend bewiesen worden, dass die mechanischen Eigenschaften des Gebirges nicht durch Versuche kleinen Maßstabes, sondern nur großmaßstäblich ermittelt werden können. Dies hat seinen Grund darin, dass die mechanischen Gesetze statistische Gesetze sind, dass somit eine Materialprüfung nur dann sinnvoll ist, wenn der jeweilige Prüfkörper eine große Zahl von Teilkörpern (Kluftkörpern) enthält. Dazu muss er nach der Natur des Diskontinuums eine hinreichende Größe haben, welche in jeder Richtung des Raumes mindestens sechs mittlere Kluftabstände betragen muss. Die sich aus diesem Gesetz ergebenden Abmessungen sind nun einmal so groß, dass eine Prüfung im Labor schon aus Transportgründen fast ausscheidet und als einzige Möglichkeit die Prüfung in situ verbleibt.
Trotz aller Aufklärungsarbeit sind Großversuche zur Prüfung von Gesteinsfestigkeiten in situ auch heute noch selten und unbeliebt. Obwohl die Versuchstechnik ganz bedeutend vervollkommnet und verbilligt wurde und gute Ergebnisse nachgewiesen werden können, obwohl viele Objekte ohne solche Versuche gar nicht hätten gebaut werden können, entschließen sich nur wenige Ingenieure und Geologen zu ihrer konsequenten und regelmäßigen Anwendung. Offenbar hofft man immer noch, aus den Elementen Substanzfestigkeit und Reibung auf den Klüften die Massenfestigkeit eines Gebirgskörpers errechnen zu können.
Auch beim in situ Versuch stellt sich, wie bei der Probennahme für Laborversuche, das Problem der Repräsentativität. Da bei der Verwertung der Versuchsergebnisse in Standsicherheitsnachweisen und Berechnungen auf eine Klasseneinteilung nicht verzichtet werden kann, sollten bereits die Versuche in solchen Bereichen stattfinden, welche für gewisse Gebirgsfestigkeitsklassen als repräsentativ gelten dürfen. Diese Klasseneinteilung kann weder vom Geomechaniker noch vom Baugeologen allein vorgenommen werden, sie muss gemeinsam erarbeitet werden, da sie ebenso die Statik des Bauwerkes und die Sicherheitsbedingungen wie auch die Gefügeverhältnisse und die felsmechanischen Grundsätze berücksichtigen muss. Sie setzt außerdem ein gewissenhaftes Studium der Homogenbereiche in gesteins- und gefügekundlicher Hinsicht voraus.
Seitdem Leopold Müller und Mitarbeiter beim Bau der Talsperre Kurobe (Japan) Triaxialversuche in situ durchgeführt haben, zählen solche Versuche zum Standardrepertoir des in situ Versuchswesens. Bei diesen Versuchen wird entweder der Probekörper aus dem Gebirge herausgearbeitet und dann mit Hydraulikzylindern echt dreiaxial getestet, oder es wird eine Versuchsvariante gewählt, bei der der Versuchskörper axial mit hydraulischen Pressen belastet wird und die mittlere und kleinste Hauptnormalspannung mittels Druckkissen aufgebracht werden (s. Abb. 1 und 2).
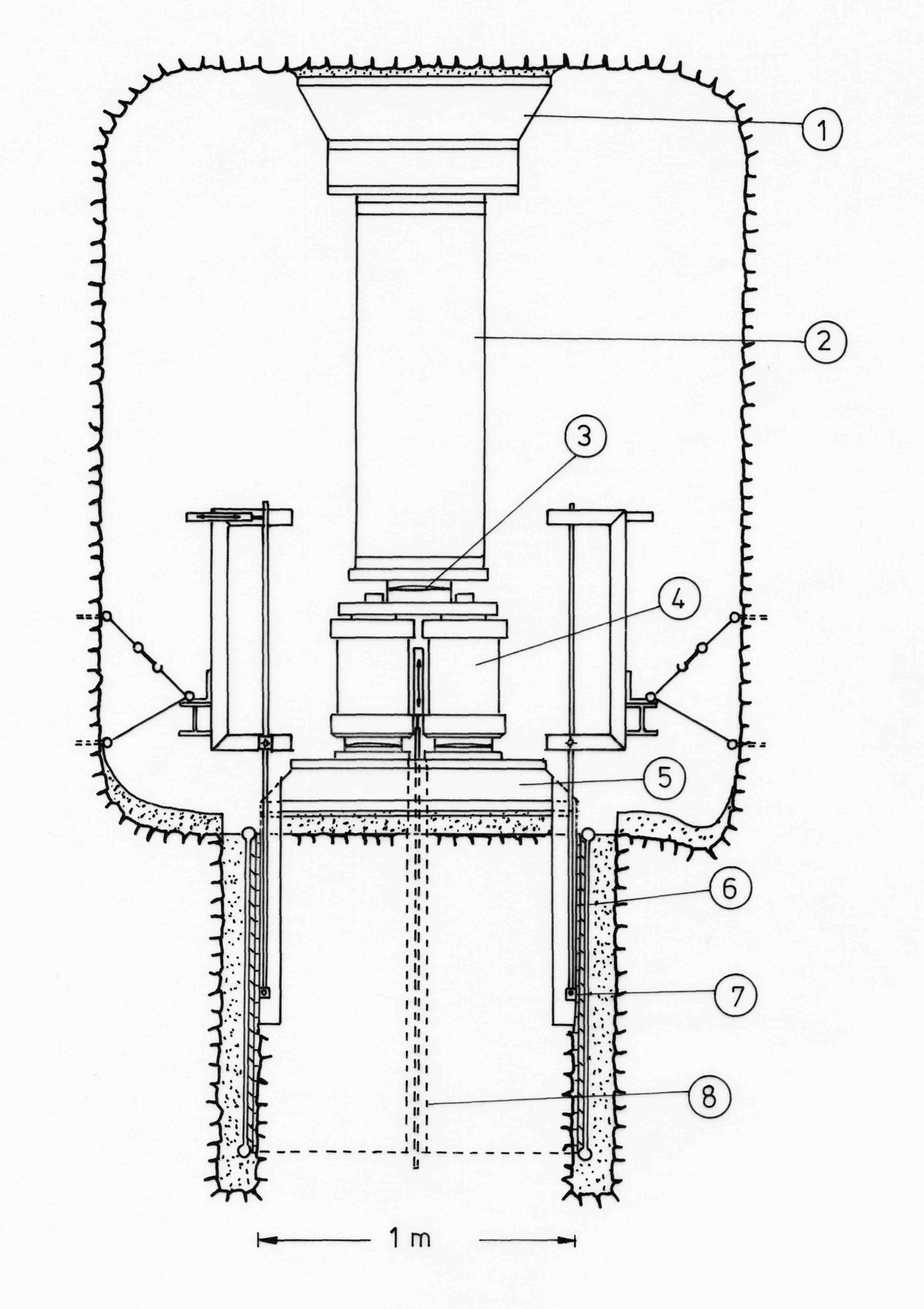
Abb. 1 In situ Triaxialversuch an einem Probekörper von 1 x 1 x 1 m.
1 Widerlager in der Firste des Versuchsstollens
2 Reaktionsbalken
3 Kugelkalotte
4 3 Druckzylinder à 1,5 MN
5 Lastverteilplatte
6 Druckkissen mit maximalem Kissendruck von 100 bar
7 Horizontalwegmessung
8 Vertikalwegmessung
Der Schlitz für die Druckkissen wird mit Hilfe einer Schlitzbohrvorrichtung gebohrt (Abb. 3), das Kissen wird eingesetzt und der verbleibende Hohlraum mit Zementmörtel verfüllt. Die Druckkissen sind belastbar bis 100 bar und mehr. Die Verformungen des Probekörpers in Richtung der mittleren und kleinsten Hauptnormalspannungen werden mit je einem Deflektometer in Bohrungen innerhalb des Probekörpers gemessen. In axialer Richtung werden die Verformungen an der Lastverteilplatte mit vier elektrischen Wegaufnehmern registriert.
Durch Messen der Verformungen in allen drei orthogonalen Achsrichtungen des Prüfkörpers mittels Deflektometern und Extensometern sowie der Randspannungen (Druckkissendrücke, Drücke aus Pressenkräften) lassen sich Verformungsmoduli und Querdehnungszahlen in den verschiedenen Richtungen bestimmen. Dadurch, dass sich die Belastungen in den drei Achsrichtungen getrennt steuern lassen, kann eine Vielzahl von Spannungszuständen im Prüfkörper erzeugt werden.
Mit Hilfe der beschriebenen Verschiebungsmesseinrichtungen ist es sodann möglich, das Verformungsverhalten der anisotropen Felsprobe bei Veränderung der Spannungszustände zu studieren. Spannungen und Dehnungen ergeben sich als für den Probenmittelpunkt repräsentative Werte. Die jeweils auf einer ganzen Probenkörperseite aufgebrachten Flächenbelastungen garantieren, dass zumindest in der Umgebung des Probenmittelpunktes der Spannungszustand vorliegt, dessen Hauptachsen den drei Richtungen der Belastungen entsprechen. Mit ausreichender Genauigkeit kann davon ausgegangen werden, dass Verzerrungen des induzierten Spannungszustandes nur in den Ecken des Körpers auftreten.
Von den in den übrigen Kapiteln besprochenen Versuchen ist der dreiachsige Druckversuch am besten zur Gewinnung von Kennwerten für Berechnungen mittels numerischer Rechenverfahren geeignet, da aus diesem Versuch sowohl Festigkeitswerte (Grenzbedingung des Materials) als auch Spannungs-Dehnungsbeziehungen abgeleitet werden können.

Abb. 2 Axiale Lastaufbringung mit drei Hydraulikzylindern

Abb. 3 Herstellung des Probekörpers durch Loch-an-Loch-Bohrungen

Abb. 4 Triaxialversuch im Zugangsstollen der Kaverne Cirata, Indonesien
Die komplette Beschreibung zu In situ Triaxialversuche finden Sie auch hier als pdf.

